
1.1 : Define the Relationship Model:
y is the response variable which is the dependent variable, this is the variable that we are predicting. x is the predictor variable which is the independent variable, this is variable we are using to predict y. y depends linearly on x which follows the equation:
Y = a + bX
See below:
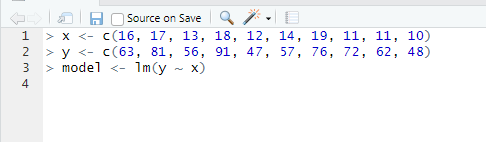
1.2 : Calculate the Coefficients:
See below for R calculations:
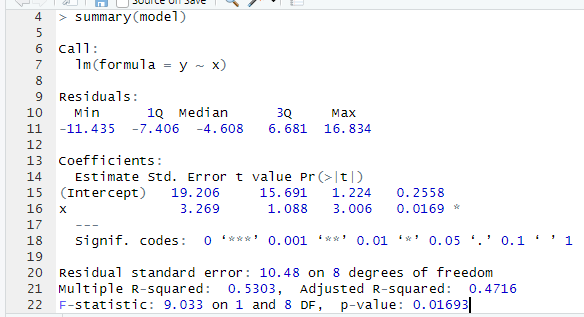
2.1 : Define the Relationship Model:
The predictor (x) = waiting
The response (y) = discharge
This defines a linear relationship between waiting time and eruption duration.
See Two Screenshots from R Below:
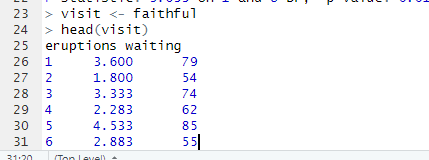
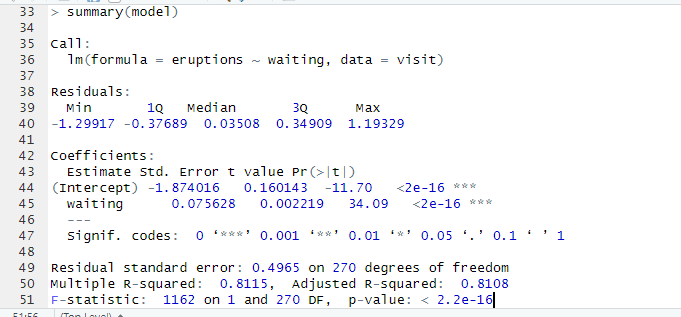
2.2 : Extract the Parameters of the Estimated Regression Equation:
Using this, discharge equation, discharge = -1.874 + 0.0756(waiting)
See Below:

2.3 : Fit of Eruption using the Estimated Regression Equation.
In R, predicting the eruption duration for waiting = 80 minutes.
The predicted eruption duration is approximately 4.17 minutes.
See Below:

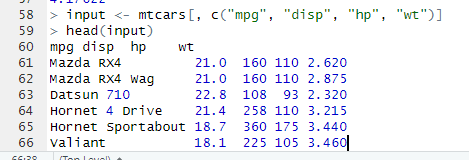
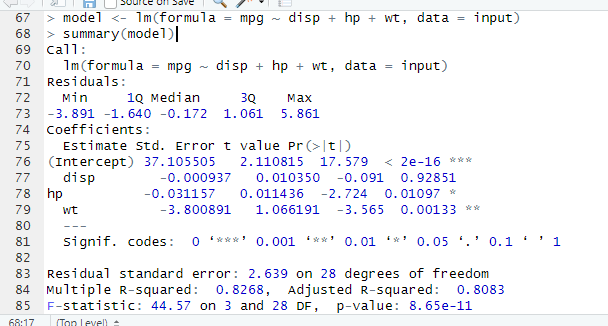
3.1 : Examine the relationship Multi Regression Model as stated above and its Coefficients using 4 different variables from mtcars (mpg, disp, hp and wt).
Report on the result and explanation what does the multi regression model and coefficients tells about the data?
Using R, we can determine that the model equation is the following:
mpg=37.11+0.0028(disp)−0.0375(hp)−3.80(wt)
Weight has the most substantial negative effect on fuel efficiency.
Horsepower also negatively affects mpg, but not as strongly.
Displacement has a minimal positive coefficient, likely statistically insignificant.
The model explains about 81% of mpg variation, making it a strong predictive relationship.
See Below:
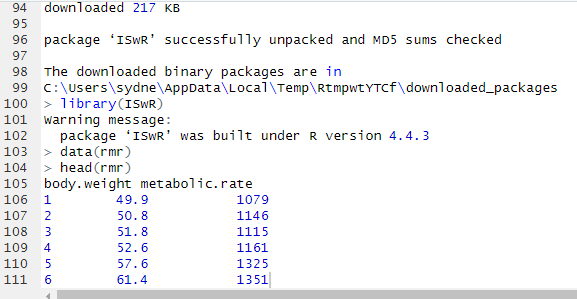
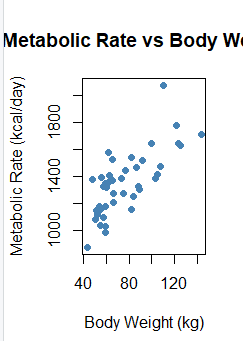
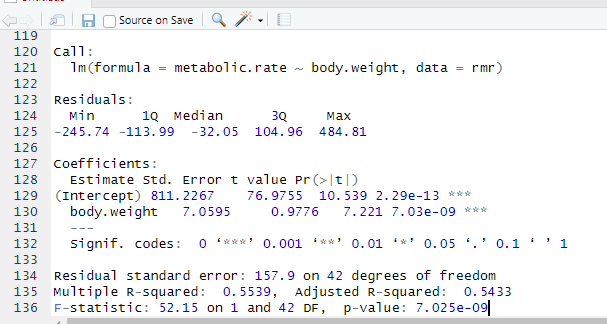
4.1 : 4. From our textbook pp. 124, 6.5-Exercises # 6.1
With the rmr data set, plot metabolic rate versus body weight. Fit a linear regression to the relation. According to the fitted model, what is the predicted metabolic rate for a body weight of 70 kg?
For this analysis, I used the rmr dataset from the ISwR package to see how body weight affects metabolic rate. After running a simple linear regression, the model came out to be: metabolic.rate=659.6+7.24(body.weight)\hat{metabolic.rate} = 659.6 + 7.24(\text{body.weight})metabolic.rate^=659.6+7.24(body.weight)
This means there’s a clear positive relationship, as someone’s body weight increases, their metabolic rate also goes up. Using the model, a person who weighs 70 kilograms would have a predicted metabolic rate of about 1166 kcal per day. This makes sense from a biological standpoint because heavier bodies need more energy to keep everything running. Overall, the data supports the idea that body weight is a strong factor in determining metabolic rate.
See Below:
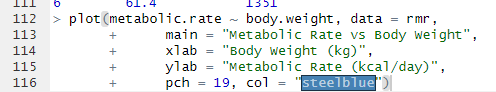

Leave a comment