Sydney – LIS4273

A1. Event A = row A = 10 + 20 = 30

P(A)=30/90=0.333 = 33.3%

A2. Event B = column B = 10 + 20 = 30

P(B)=30/90=0.333 = 33.3%

A3. We need P(A∪B)

• P(A)=30/90
• P(B)=30/90
• P(A∩B)=10/90

P(A∪B)=P(A)+P(B)−P(A∩B) : 30/90 + 30/90 -10/90 = 50/90 = .556 = 55.6%

A4. P(A or B) = P(A) + P(B)?

• P(A∪B)=0.556
• P(A)+P(B)=0.666 Answer: False

B1. This answer is True.

B2. This result happens because rain is rare, happening only 5 out of 365 days. Even though the weatherman is 90% accurate when it does rain, the large number of nonrainy days makes most rain predictions false alarms. Therefore, the overall chance of actual rain given a rain forecast is only 11%.

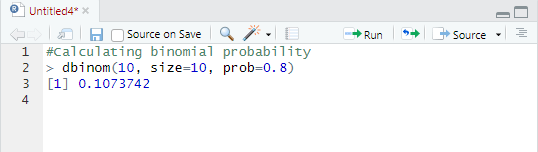
P=0.107 (10.7% chance of all 10 successes).